FI – Matematiikka, pitkä oppimäärä
20.3.2024
Koe koostuu 13 tehtävästä, joista vastataan kymmeneen. Tehtävät on jaettu kolmeen osaan. A-osassa on neljä kaikille pakollista tehtävää. B1-osassa on viisi tehtävää, joista vastataan kolmeen. B2-osassa on neljä tehtävää, joista vastataan kolmeen. Kaikki tehtävät arvostellaan pistein 0–12, joten kokeen maksimipistemäärä on 120.
A-osassa saat käyttää koejärjestelmässä olevaa taulukkokirjaa ja perusohjelmia. A-osa palautetaan tehtävän 4 jälkeen olevalla painikkeella. Tämän jälkeen A-osan vastauksia ei voi enää muokata. A-osan palauttamisen jälkeen kaikki koejärjestelmän ohjelmat ovat käytettävissäsi. Voit vastata B-osien tehtäviin myös ennen A-osan palauttamista.
Useimmissa tehtävissä kaikkien osatehtävien vastaukset kirjoitetaan samaan vastauskenttään. Jaottele vastauksesi osatehtävien mukaisesti. Halutessasi voit tuottaa vastausten tueksi piirroksia, kaavioita tai taulukoita ja liittää niistä kuvakaappauksen mihin tahansa tekstivastaukseen.
Älä jätä mitään merkintöjä sellaisen tehtävän vastaukselle varattuun tilaan, jota et halua jättää arvosteltavaksi.
A-osa
Vastaa neljään tehtävään.1. Kulmanmetsästys 12 p.
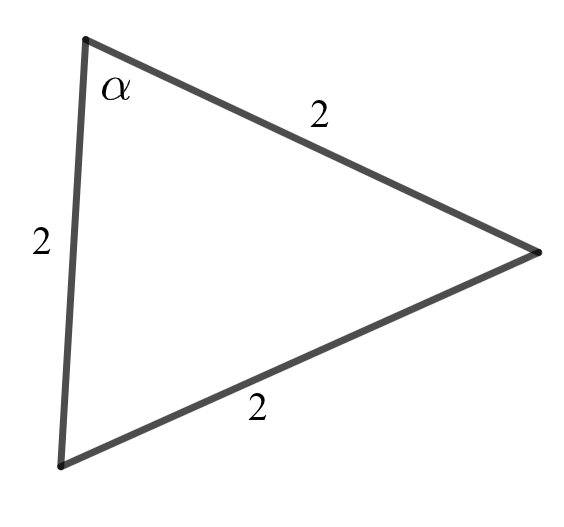
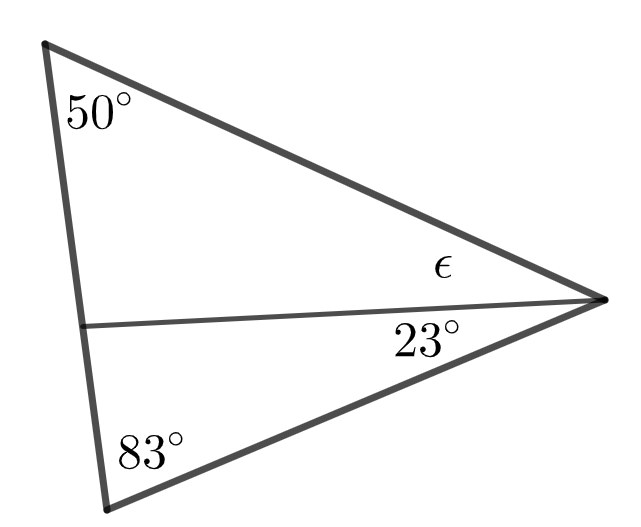
Määritä kuviin merkityt tuntemattomat kulmat asteen tarkkuudella.
Kirjoita tämän tehtävän vastauskenttiin pelkät laskujen lopputulokset ilman välivaiheita ja perusteluja. Jokaisen kohdan vastaus on kokonaisluku.
1.1 Määritä kulma \alpha. 2 p.
\alpha = astetta
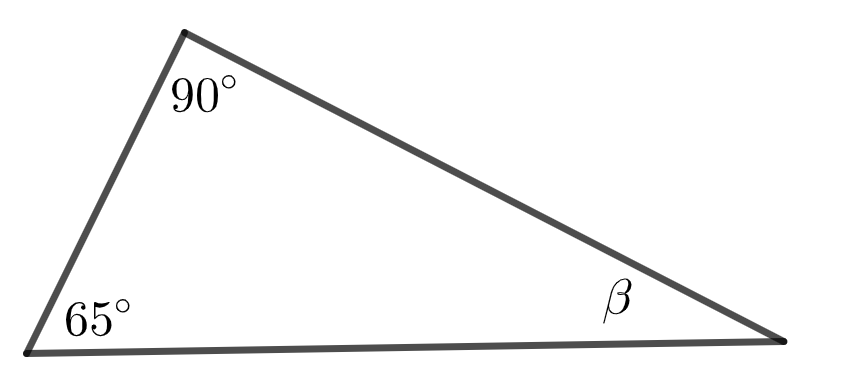
1.2 Määritä kulma \beta. 2 p.
\beta = astetta
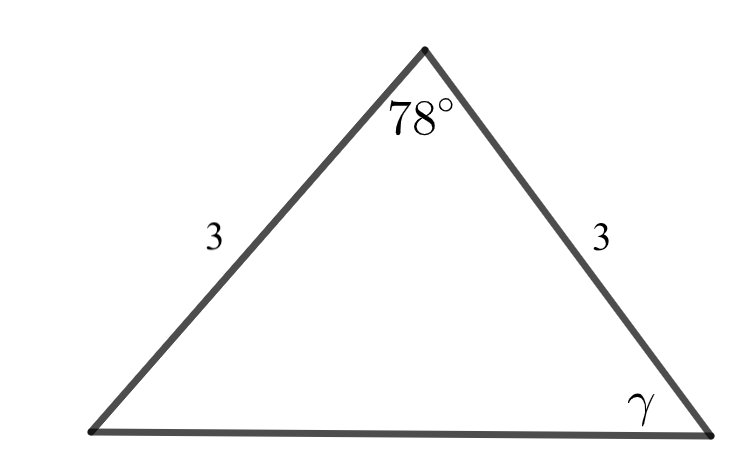
1.3 Määritä kulma \gamma. 2 p.
\gamma = astetta
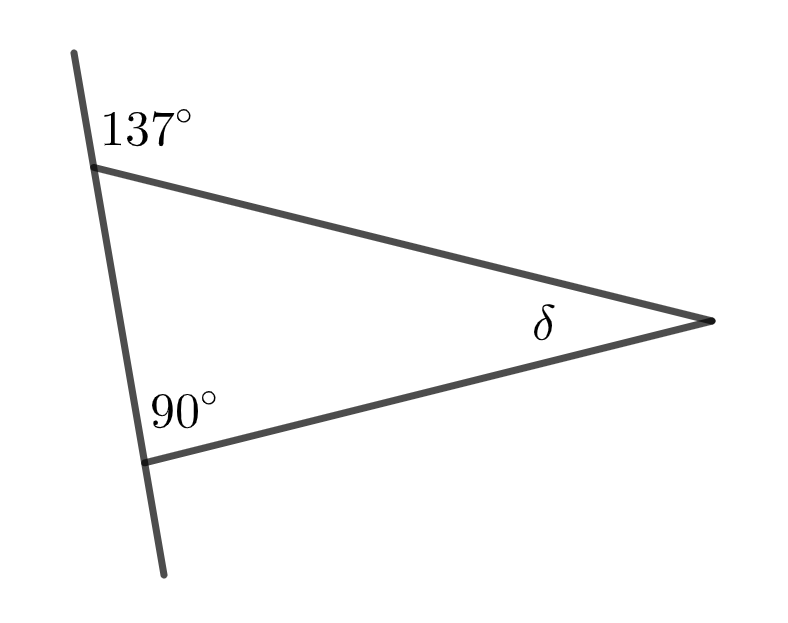
1.4 Määritä kulma \delta. 2 p.
\delta = astetta
1.5 Määritä kulma \epsilon. 2 p.
\epsilon = astetta
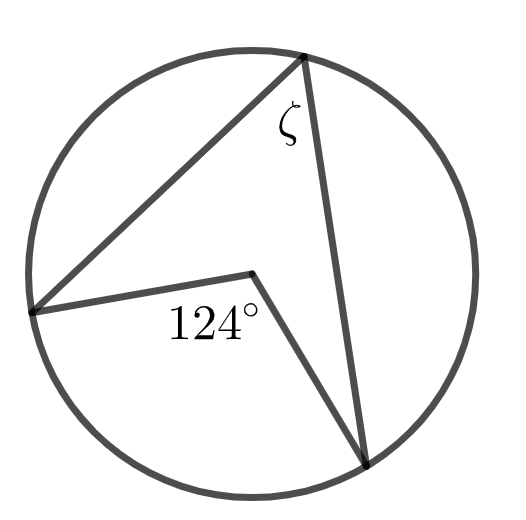
1.6 Määritä kulma \zeta. 2 p.
\zeta = astetta
2. Polynomi 12 p.
Kirjoita tämän tehtävän vastauskenttiin pelkät laskujen lopputulokset ilman välivaiheita ja perusteluja. Jokaisen kohdan vastaus on kokonaisluku.
Laske polynomin p(x) =12 x^3 +4 x arvo kohdassa x =2.
3 p.Laske polynomin p(x) =12 x^3 +4 x derivaatan arvo kohdassa x =1.
3 p.Laske määrätty integraali int_1^2 (12 x^3 +4 x) dx.
3 p.Määritä neljännen asteen termin kerroin polynomissa (12 x^3 +4 x)^2.
3 p.
3. Itseisarvoyhtälöitä 12 p.
Ratkaise algebrallisesti tai geometrisesti seuraavat yhtälöt.
|y +3| =|y +5|. (6 p.)
|x| +|x -5| =7. (6 p.)
4. Laskuvarjohyppääjä 12 p.
Mallinnetaan laskuvarjohyppääjän putoamisnopeutta funktiolla
v(t) =80 (e^(t/4) -1) /(e^(t/4) +1),
kun aikaa t mitataan sekunneissa hyppäyshetkestä t =0 alkaen ja nopeuden yksikkö on metriä sekunnissa.
Johda derivaattakaava
D(8 ln(e^(t/4) +1) -t) =(e^(t/4) -1) /(e^(t/4) +1).
Määritä hyppääjän ensimmäisen 20 sekunnin aikana putoama matka, joka saadaan integraalista
h =int_0^20 v(t) dt.
Voit käydä tarkastelemassa A-osan vastauksiasi nyt.
Palautettuasi A-osan et voi enää muokata A-osan vastauksia.
Tarkastelun jälkeen voit palata kokeeseen jatkamaan tehtäviin vastaamista.
•••
Saat estetyt laskinohjelmat käyttöösi palautettuasi A-osan.
B1-osa
Vastaa kolmeen tehtävään.5. Lämpötilaruudukko 12 p.
Aineisto
Lämpötilajakaumaa voidaan mallintaa ruudukolla, jossa ruudussa oleva luku on kyseisen ruudun lämpötila celsiusasteina. Lämpötilat noudattavat seuraavaa keskiarvoperiaatetta: jokaisen ruudun lämpötila on neljän naapuriruudun lämpötilan keskiarvo. Ruudut ovat naapuriruutuja, jos niillä on yhteinen sivu.
Tässä tehtävässä tutkitaan taulukon 5.A tilannetta. Siinä esimerkiksi lämpötila 15 toteuttaa keskiarvoperiaatteen mukaisen yhtälön
(0 +10 +20 +30) /4 =15.
Muodosta ruudukon tuntemattomille lämpötiloille x ja y keskiarvoperiaatteen mukaiset yhtälöt ja ratkaise ne.
6. Piste hukassa 12 p.
Tason pisteen C etäisyys pisteestä A =(5, 4) on sqrt(20) ja etäisyys pisteestä B =(8, -2) on sqrt(65). Lisäksi pisteen C etäisyys pisteen B kautta kulkevasta, vektorin 5 vec i +2 vec j suuntaisesta suorasta s on alle 7. Määritä pisteen C koordinaatit sekä pisteen C tarkka etäisyys suorasta s.
7. Scrabble 12 p.
Englanninkielisessä Scrabble-pelissä pussissa on 100 laattaa, joista 2 on tyhjää, 56 konsonanttilaattaa ja 42 vokaalilaattaa. Vokaalilaatoista yhdeksässä on A-kirjain. Pelaaja nostaa pussista 7 laattaa palauttamatta niitä takaisin pussiin.
Millä todennäköisyydellä ainakin yhdessä pelaajan nostamista laatoista on A-kirjain? (6 p.)
Millä todennäköisyydellä ainakin yhdessä pelaajan nostamista laatoista on A-kirjain silloin, kun tiedetään pelaajan nostaneen kolme vokaalia? (6 p.)
8. Taivaanmekaniikka 12 p.
Aineisto
Maapallo pyörii akselinsa ympäri. Akselin ja Maan kiertoradan tason (eli ratatason) normaalin välisen kulman suuruus on 23,5 astetta, ja akselin suunta pysyy samana Maan kiertäessä Aurinkoa. Akselin asento on sellainen, että pohjoisnapa on kesäpäivänseisauksena lähimpänä Aurinkoa ja talvipäivänseisauksena kauimpana siitä. Videossa 8.A on havainnollistettu tilannetta.
Määritä Maan akselin ja Auringosta Maahan kulkevan säteen välinen kulma kuukausi kesäpäivänseisauksen jälkeen. Maapallon kiertorata oletetaan tässä ympyräksi.
9. Kääntyvä, muttei monotoninen 12 p.
Anna esimerkki funktiosta f: A -> B, jolla on käänteisfunktio, mutta joka ei ole monotoninen. Muista kertoa, mitkä ovat funktiosi määrittelyjoukko A ja arvojoukko B.
B2-osa
Vastaa kolmeen tehtävään.10. Tekoäly ja lukuteorian ihmeet 12 p.
Aineisto
Alkulukua q kutsutaan alkulukukaksoseksi, jos myös q +2 tai q -2 on alkuluku. Tekoälyltä kysyttiin, kuinka monta alkulukukaksosta on olemassa, ja sen vastaus on tekstissä 10.A. Vastaa aineiston pohjalta seuraaviin osatehtäviin.
Anna esimerkki alkuluvusta, joka ei ole alkulukukaksonen. (3 p.)
Onko tekoälyn alkulukukaksosen määritelmä yhtäpitävä tehtävän määritelmän kanssa? (3 p.)
Onko tekoälyn perustelu alkulukukaksosten lukumäärän äärettömyydelle matemaattisesti pätevä? (6 p.)
11. Brownin liike 12 p.
Vuonna 1827 kasvitieteilijä Robert Brown tutki mikroskoopilla, miten siitepölyhiukkanen liikkuu nykien vedessä. Brownin koe viittasi molekyylien olemassaoloon, ja sillä oli siten tärkeä rooli atomiteorian historiassa.
Tutkitaan yksinkertaistettua Brownin liikettä. Hiukkasen liike tasossa alkaa origosta. Tasaisin väliajoin hiukkanen liikkuu yhden yksikön verran joko ylös, alas, oikealle tai vasemmalle. Jokaisen suunnan todennäköisyys on 1/4. Esimerkiksi ensimmäisen askeleen jälkeen mahdolliset sijainnit ovat (0, 1), (0, -1), (1, 0) ja (-1, 0).
Tutkitaan hiukkasen sijaintia neljän askeleen jälkeen. Kutsutaan tätä päätepisteeksi.
Määritä päätepisteen kaikki mahdolliset x-koordinaatit sekä niiden todennäköisyydet.
12. Potensseja aritmeettisissa lukujonoissa 12 p.
Olkoon k > 0 kokonaisluku. Osoita, että jos päättymätön kasvava aritmeettinen lukujono sisältää luvut k^2 ja k^3, niin se sisältää luvun k^4. (6 p.)
Osoita, että jos r^2, r^3 ja r^4 sisältyvät aritmeettiseen lukujonoon, niin r on rationaaliluku. (6 p.)
13. Raja-arvo 12 p.
Ohjelmiston mukaan
lim_(x -> 0) (1 /x^2 –(sin x) /x^3) =1/6.
Perustele tämä tulos seuraavien välivaiheiden avulla.
[i] Osoita, että x -sin x -1/6 x^3 <= 0. kun 0 <= x <= 1.
[ii] Osoita, että x -sin x -1/6 x^3 +1/120 x^5 <= 0, kun 0 <= x <= 1.
[iii] Osoita, että 1/6 x^3 -1/120 x^5 <= x -sin x <= 1/6 x^3, kun 0 <= x <= 1.
[iv] Osoita, että 1/6 x^3 -1/120 x^5 <= x -sin x >= 1/6 x^3, kun -1 <= x <=0.
[v] Perustele näiden epäyhtälöiden avulla, että raja-arvo on 1/6.
Välivaiheita voi perustella toisistaan riippumattomasti. Esimerkiksi vaiheen [iv] osapisteet saa osoittamalla, että se seuraa vaiheesta [iii], riippumatta siitä, onko vaihe [iii] todistettu. Sama pätee muihinkin vaiheisiin.
Kokeen tehtävät loppuvat tähän.