Aineisto: FI – Fysiikka

2.A  Mittausaineisto: McLaughlin: 400 metrin aitajuoksun juoksuvauhti ajan funktiona

t (s)	v (m/s)
0	0
3.06	7.365
8.13	8.685
12.25	8.294
16.49	8.235
20.83	7.883
25.33	7.675
29.94	7.527
34.6	7.495
39.3	7.384
44.09	7.246
49.2	7.407
51.9	7.820

Jokainen alla oleva tiedosto sisältää samat tiedot. Tallenna tiedosto, käynnistä valitsemasi ohjelmisto ja avaa tallentamasi tiedosto ohjelmiston valikosta.

2A.ods (LibreOffice Calc)

2A.cmbl (Logger Pro)

2A.ggb (GeoGebra)

2A.vcp (Casio ClassPad Manager)

2A.tns (TI-Nspire)

2.B  Mittausaineisto: Muhammad: 400 metrin aitajuoksun juoksuvauhti ajan funktiona

t (s)	v (m/s)
0	0
3.04	7.401
8.06	8.838
12.14	8.353
16.39	8.121
20.76	7.901
25.24	7.709
29.8	7.659
34.41	7.511
39.19	7.157
44.11	7.071
49.5	6.849
52.42	7.080

Jokainen alla oleva tiedosto sisältää samat tiedot. Tallenna tiedosto, käynnistä valitsemasi ohjelmisto ja avaa tallentamasi tiedosto ohjelmiston valikosta.

2B.ods (LibreOffice Calc)

2B.cmbl (Logger Pro)

2B.ggb (GeoGebra)

2B.vcp (Casio ClassPad Manager)

2B.tns (TI-Nspire)

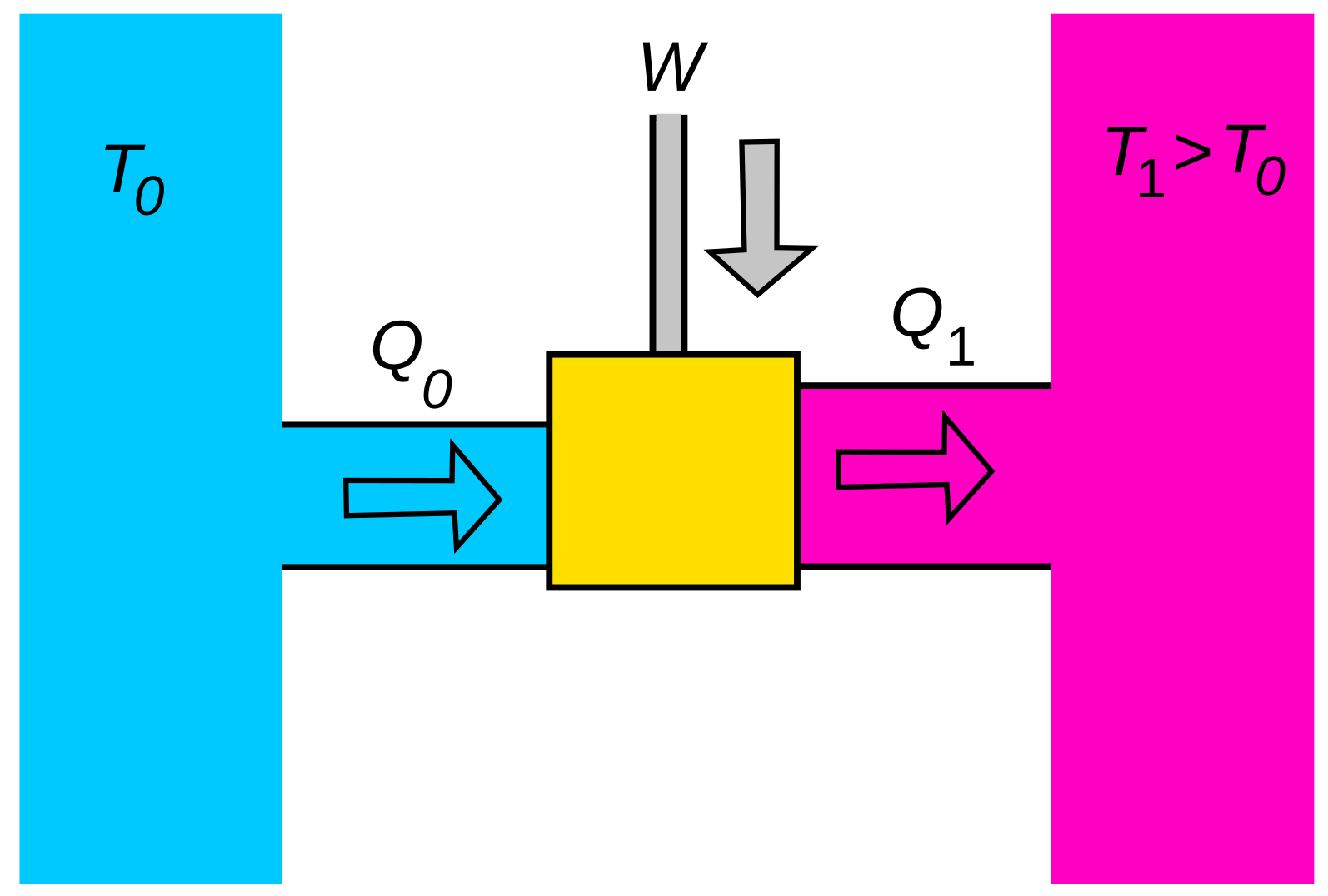
3.A  Kuva: Ilmalämpöpumpun energiavirtakaavio

5.A  Taulukko: Mars, Phobos ja Deimos

Taivaankappale	Massa (kg)	Kiertoradan säde (m)	Kiertoaika (d)
Mars	6,4171 · 1023	—	—
Phobos	1,08 · 1016	9,3772 · 106	0,319
Deimos	1,80 · 1015	2,34632 · 107	1,263

5.B  Animaatio: Phobosin ja Deimosin kiertoradat Marsin ympäri

7.A  Kuva: Sähkölukko

8.A  Teksti ja kuva: Kevyiden ytimien synty

Monet maailmankaikkeudesta tehdyt havainnot selittyvät alkuräjähdyksellä eli sillä, että kaikki alkoi tiheästä ja kuumasta alkutilasta noin 14 miljardia vuotta siten. Ainetta, sellaisena kuin me sen nykyään tunnemme, ei silloin ollut. Aivan varhaisimmista vaiheista tietomme on hyvin rajallinen, mutta laboratoriokokeiden perusteella tiedämme, miten aine ja säteily käyttäytyvät olosuhteissa, jotka vallitsivat maailmankaikkeuden ollessa miljoonasosasekunnin ikäinen ja sen jälkeen.

Maailmankaikkeuden ehdittyä noin yhden sekunnin ikään sen lämpötila oli noin T=1,0\cdot 10^{10}\,{\rm K}. Tuolloin oli jo ehtinyt syntyä protoneja ja neutroneja. Neutronien lukumäärän N_{\rm n} ja protonien lukumäärän N_{\rm p} suhde tässä vaiheessa voidaan arvioida yhtälöstä

\frac{N_{\rm n}}{N_{\rm p}} = \exp\bigl(-\frac{\Delta mc^2}{kT}\bigr)

jossa \Delta m>0 on neutronin ja protonin massojen erotus, c on valonnopeus ja k on Boltzmannin vakio. Neutronien osuus nukleoneista esitetään suhteena R=N_{\rm n}/(N_{\rm n}+N_{\rm p}). Suhteen R avulla voidaan ennustaa kevyiden isotooppien syntymistä.

Ajan kuluessa maailmankaikkeus jäähtyi noin 10^9\,{\rm K}:iin ja protoneista ja neutroneista koostuville atomiytimille tuli mahdolliseksi pysyä koossa. Vedyn kevyintä isotooppia (protoni) oli olemassa jo ennestään. Seuraavien kymmenien minuuttien aikana syntyi muita kevyitä ytimiä, tässä vaiheessa vedyn, heliumin ja litiumin isotooppeja. Näin syntyneiden kevyiden ydinten suhteelliset osuudet voidaan laskea, kun tunnetaan ydinreaktiot, joissa niitä syntyy.

Edellä kuvatuissa vaiheissa aineen keskitiheys oli hyvin suuri. Sen jälkeen maailmankaikkeus jatkoi laajenemistaan ja aineen tiheys pieneni. Oheisessa kuvassa on vaaka-akselilla tavallisen aineen tiheys avaruudessa suhteessa fotonien tiheyteen. Käyrät ovat teoreettinen ennuste, joka kertoo alkuräjähdyksessä syntyneiden kevyiden isotooppien massaosuudet S tiheyden funktiona, pystyakselin yksikkönä vedyn massaosuus S_{\rm o}. Kuvan pystysuora viiva on sellaisen tiheyden kohdalla, joka vastaa NASA:n WMAP-satelliitin massaosuuksista tekemiä havaintoja. Ne on kuvassa merkitty ympyröin.

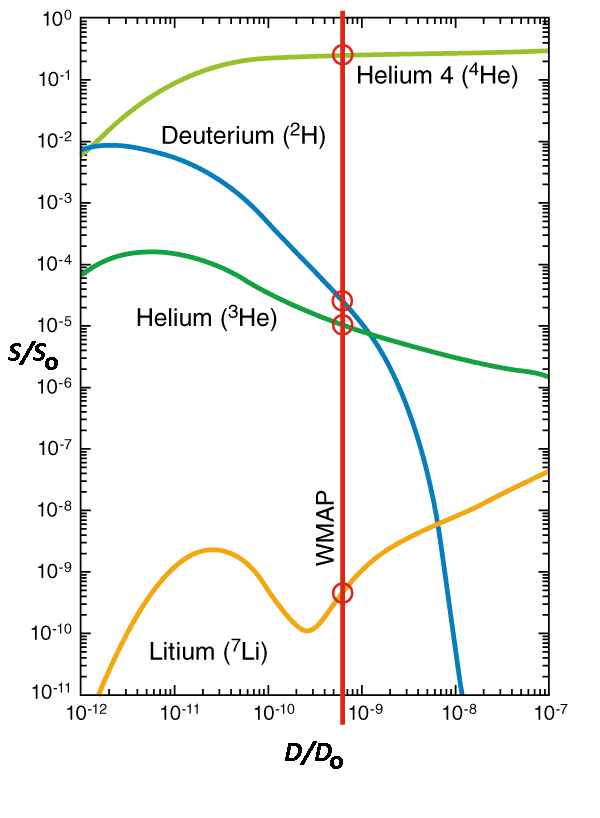Kevyiden ydinten suhteelliset massaosuudet S avaruudessa tiheyden D funktiona. Vakio S_{\rm o} on valittu siten, että pystyakselin yksikkö on vedyn suhteellinen massaosuus. Vakio D_{\rm o} on fotoneihin liittyvä tiheysparametri. Pystysuoralla viivalla on WMAP-satelliitin havainnot.

9.A  Taulukko: Trampoliinilla hyppivän fyysikon sijainti ajan funktiona

Jokainen alla oleva tiedosto sisältää samat tiedot. Tallenna tiedosto, käynnistä valitsemasi ohjelmisto ja avaa tallentamasi tiedosto ohjelmiston valikosta.

9A.ods (LibreOffice Calc)

9A.cmbl (Logger Pro)

9A.ggb (GeoGebra)

9A.vcp (Casio ClassPad Manager)

9A.tns (TI-Nspire)

9.B  Teksti: Trampoliinilla hyppimisen mekaniikkaa

Kun trampoliinilla hyppivä ihminen on kosketuksissa trampoliinin pintaan, trampoliini kohdistaa häneen ylöspäin suuntautuvan voiman. Tämä voima riippuu paikasta y

F(y)=-ky,

jossa k on trampoliinin ”jousivakio” ja y pystysuuntainen poikkeama kuormittamattoman trampoliinin tasosta (positiivinen suunta ylöspäin). Toisaalta hyppijään vaikuttaa myös paino mg, jossa m on hyppijän massa ja g putoamiskiihtyvyys. Tasapainossa nämä kaksi voimaa ovat yhtä suuret. Tasapainotilanne saavutetaan esimerkiksi astumalla trampoliinille varovasti ja odottamalla, että värähdysliike vaimenee. Toisaalta tasapainoaseman ympärillä voi myös helposti ylläpitää pientä värähdysliikettä, jonka taajuus f on

f=\frac{1}{2\pi}\sqrt{\frac{k}{m}}.

Tällöin hyppijän paikkaa ajan funktiona esittää yhtälö

y(t)=-\frac{mg}{k}-A\cos(2\pi f t),

jossa A on värähdysliikkeen amplitudi. Vastaavasti hyppijän nopeus ajan funktiona on

v(t)=2\pi f A\cdot\sin(2\pi f t).

Trampoliinin hyppijään kohdistama voima voi suuntautua vain ylöspäin, joten liike on pelkkää värähdysliikettä vain pienillä amplitudeilla. Suurilla amplitudeilla hyppijä irtoaa välillä trampoliinista.

10.A  Kuva: Täysi vesipullo

10.B  Taulukko: Veden lämpötila ajan funktiona

Jokainen alla oleva tiedosto sisältää samat tiedot. Tallenna tiedosto, käynnistä valitsemasi ohjelmisto ja avaa tallentamasi tiedosto ohjelmiston valikosta.

10B.ods (LibreOffice Calc)

10B.cmbl (Logger Pro)

10B.ggb (GeoGebra)

10B.vcp (Casio ClassPad Manager)

10B.tns (TI-Nspire)

10.C  Kuva: Jäähdytetty tyhjä pullo

11.A  Teksti: Työselostus

11A_fi.pdf