FI – Fysiikka
22.9.2022
Koe koostuu 11 tehtävästä, joista vastataan seitsemään. Tehtävät on jaettu kolmeen osaan. Osassa 1 on yksi kaikille pakollinen 20 pisteen tehtävä. Osassa 2 on seitsemän 15 pisteen tehtävää, joista vastataan neljään. Osassa 3 on kolme 20 pisteen tehtävää, joista vastataan kahteen. Kokeen maksimipistemäärä on 120. Kaikki annetut vastaukset tulee perustella, jos perusteleminen on vastausteknisesti mahdollista. Voit tuottaa vastausten tueksi piirroksia, kaavioita tai taulukoita ja liittää niistä kuvakaappauksen mihin tahansa tekstivastaukseen.
Älä jätä mitään merkintöjä sellaisen tehtävän vastaukselle varattuun tilaan, jota et halua jättää arvosteltavaksi.
Osa 1: 20 pisteen tehtävä
Vastaa tehtävään 1.1. Monivalintatehtäviä fysiikan eri osa-alueilta 20 p.
Valitse jokaisessa osatehtävässä 1.1–1.10 parhaiten soveltuva vaihtoehto. Oikea vastaus 2 p., väärä vastaus 0 p., ei vastausta 0 p.
Osatehtävissä 1.1–1.3 tarkastellaan tilannetta, jossa lapsi hyppii trampoliinilla tehden jatkuvasti samanlaisia hyppyjä ilmaan.
1.1 Kun lapsen jalat koskettavat alastulossa trampoliinin pintaa, trampoliini alkaa hidastaa lapsen vauhtia. Mikä seuraavista väittämistä pätee tilanteessa? 2 p.
1.2 Trampoliinin venymä on suurimmillaan ja lapsen liikkeen suunta on juuri vaihtumassa. Mikä seuraavista väittämistä pätee tilanteessa? 2 p.
1.3 Lapsi on noussut ilmaan uuteen hyppyyn. Mikä seuraavista väittämistä kuvaa parhaiten lapsen liikettä trampoliinista irtoamisen jälkeen? 2 p.
1.4 Kun kaksi metallikappaletta on kosketuksissa toistensa kanssa, havaitaan että niiden välillä ei siirry energiaa lämpönä. Mikä seuraavista väittämistä pitää varmasti paikkansa tilanteessa? 2 p.
1.5 Mitä eroa on veden kiehumisella ja veden höyrystymisellä? 2 p.
1.6 Miten sähköstaattinen pölyhuiska saa sähkövarauksensa? 2 p.
1.7 Miksi sähköstaattinen pölyhuiska vetää puoleensa ilmassa leijuvia pölyhiukkasia? 2 p.
1.8 Pienellä nappimagneetilla voi kiinnittää jääkaapin oveen yhden paperiarkin mutta ei kymmenen paperiarkin nippua. Mikä seuraavista on merkittävin syy tähän? 2 p.
1.9 Auringonvalo osuu metallilevyyn lämmittäen sitä. Mikä seuraavista väittämistä pitää paikkansa energian siirtyessä valosta metallilevyyn? 2 p.
1.10 Mikä seuraavista väittämistä pätee atomiytimen radioaktiivisessa hajoamisessa? 2 p.
Osa 2: 15 pisteen tehtävät
Vastaa neljään tehtävään.2. Astronautin hyppy 15 p.
2.1 Laadi graafinen esitys määritetystä etäisyydestä ajan funktiona. Esityksessä tulee näkyä mittauspisteet ja niihin sopiva, fysikaalisen mallin mukainen sovite. Mistä liikkeen mallista on kyse? 7 p.
2.2 Millä ajanhetkellä John Young on hyppynsä korkeimmassa kohdassa? 2 p.
2.3 Määritä aineiston perusteella putoamiskiihtyvyys Kuun pinnalla. 6 p.
3. Vastapainohissi 15 p.
3.1 Määritä hissivaijerin hissikoriin ja vastapainoon kiihdytyksen aikana kohdistamat voimat. 9 p.
3.2 Kuinka suuria ovat hissin nopeus ja moottorin tuottama mekaaninen teho, kun hissin liikkeellelähdöstä on kulunut 0,80 sekuntia? 6 p.
4. Kirurginen polttolaite 15 p.
4.1 Toimenpiteessä lämmitetään ensin 1,1 g kudosnestettä ruumiinlämmöstä (37 °C) kiehumispisteeseen. Tämän jälkeen 0,40 g tästä kudosnesteestä höyrystyy. Kuinka kauan toimenpide kestää? Kudosneste on pääosin vettä. 7 p.
4.2 Tehollinen sähkövirta kudoksessa on 0,45 ampeeria. Kuinka suuri on jännitteen huippuarvo? 5 p.
4.3 Kuinka suuri on poltettavan kudosalueen resistanssi toimenpiteen aikana? 3 p.
5. Varatut kuulat 15 p.
5.1 Miksi kuulat vetävät toisiaan puoleensa ennen kosketusta? Miksi kosketus saa kuulat hylkimään toisiaan? 7 p.
5.2 Määritä, mitkä olivat kuulien varaukset ennen kuin kuulat koskettivat toisiaan. 8 p.
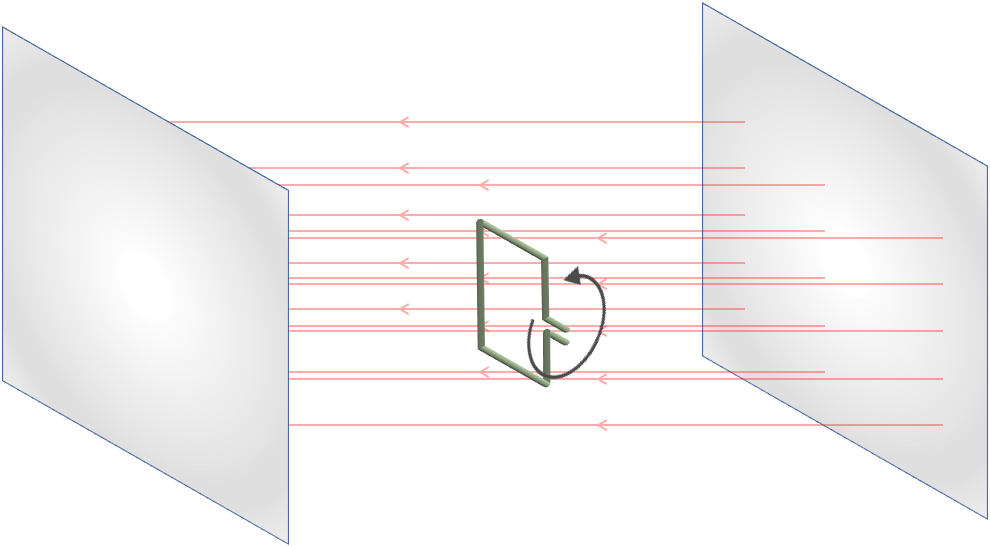
6. Sähkömagneettinen induktio 15 p.
6.1 Silmukkaa pyöritetään vakiokulmanopeudella silmukan pyörimisakselin ollessa kohtisuorassa kenttää vastaan. 3 p.
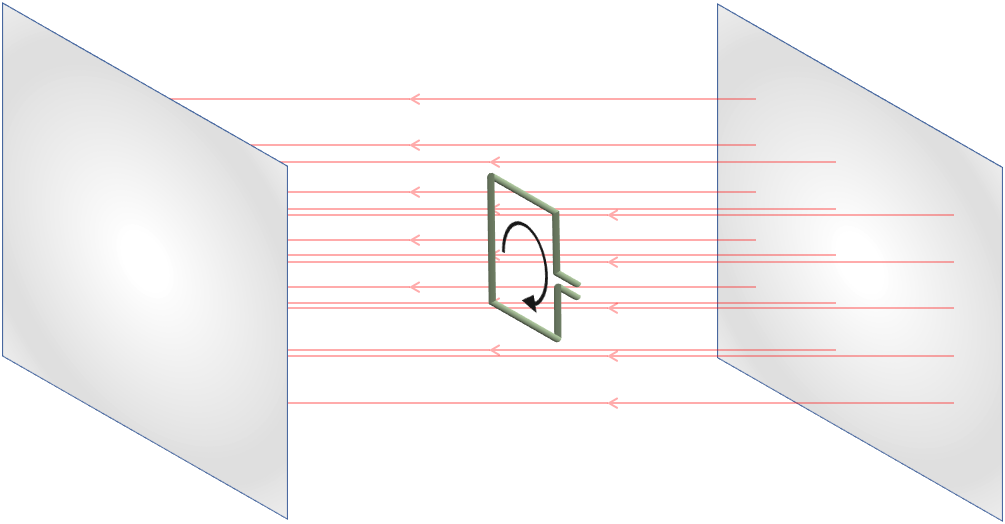
6.2 Silmukkaa pyöritetään vakiokulmanopeudella silmukan pyörimisakselin ollessa kentän suuntainen. 3 p.
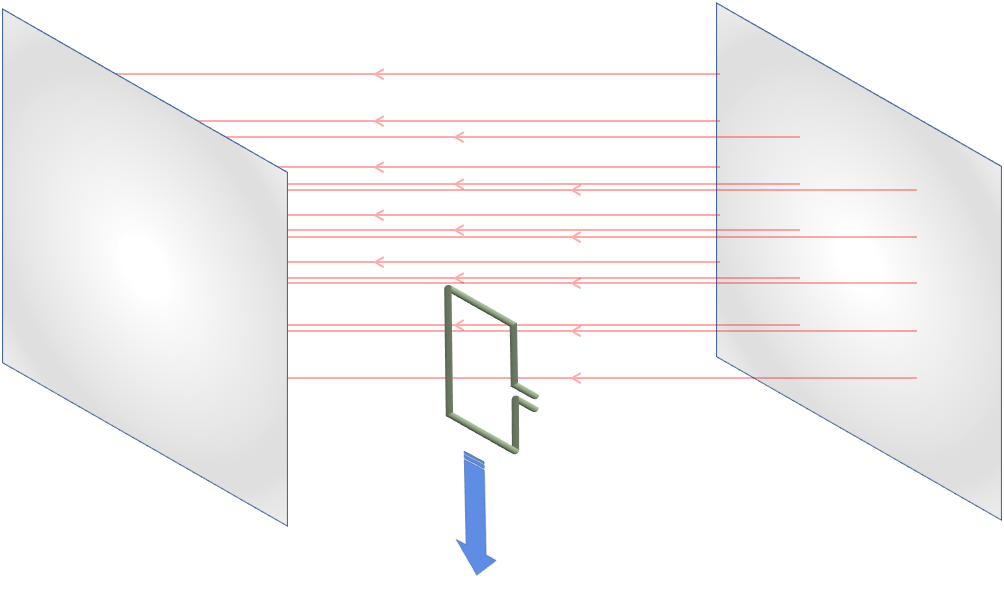
6.3 Silmukka on alussa paikallaan magneettikentän alueella. Silmukka päästetään putoamaan vapaasti nuolen suuntaan. 3 p.
6.4 Silmukka on paikallaan. Magneettikenttä häviää äkillisesti. 3 p.
6.5 Silmukka on paikallaan. Magneettikentän magneettivuon tiheys vuoron perään kasvaa ja heikkenee tasaisesti. 3 p.
7. Peltipurkkipuhelin 15 p.
7.1 Millaisena mekaanisena aaltoliikkeenä ääni etenee peltipurkkipuhelimen langassa? 2 p.
7.2
Äänen nopeudelle ohuessa messinkilangassa pätee yhtälö v = \sqrt{E/ \rho}, jossa E =10{,}5 \cdot 10^{10}~{\rm N/m}^2 on messingin kimmokerroin ja \rho =8{,}4 \cdot 10^3~{\rm kg/m}^3 tiheys. Äänen nopeus ilmassa (lämpötila 20 °C) on v_{\rm ilma}=343\ \rm{m/s}.
Kuinka paljon aiemmin ääni saavuttaa kuulijan, kun käytetään peltipurkkipuhelinta pelkän huutamisen sijaan? Peltipurkkien pituuksia ei tarvitse huomioida.
4 p.7.3
Peltipurkkipuhelimessa ääni vaimenee merkittävästi ainoastaan messinkilangassa tapahtuvan absorption takia. Vaimenemiselle pätee yhtälö I= I_1 e^{-\alpha x}, jossa I_1 on äänen intensiteetti lähteessä, I on äänen intensiteetti etäisyydellä x lähteestä ja \alpha = 0{,}086~{\rm m}^{-1} on messinkilangassa etenevän äänen vaimenemiskerroin.
Puhujan äänen intensiteettitaso on 72 dB puhujan peltipurkin pohjan kohdalla 7,0 cm:n etäisyydellä puhujan suusta. Laske äänen intensiteettitaso kuulijan peltipurkin pohjan kohdalla. Laske myös äänen intensiteettitaso 75 m:n etäisyydellä, jos puhuja puhuu samalla äänen voimakkuudella ilman peltipurkkipuhelinta. Äänen vaimeneminen ilmassa absorption takia voidaan jättää huomiotta. Vertaile tuloksia keskenään.
9 p.
8. Hiiliajoitus 15 p.
Hiili esiintyy luonnossa kahtena pysyvänä isotooppina ^{12}C ja ^{13}C sekä radioaktiivisena isotooppina ^{14}C. Ilmakehässä isotoopin ^{12}C lukumääräosuus on 98,9 % ja isotoopin ^{13}C lukumääräosuus on 1,1 %. Isotoopin ^{14}C osuus kaikesta ilmakehän hiilestä on 1{,}2 \cdot10^{-12}, ja isotoopin puoliintumisaika on 5 730 vuotta.
8.1 Isotooppi ^{14}C syntyy ilmakehässä, kun typpiydin ^{14}N sieppaa kosmisen säteilyn synnyttämän neutronin ja säteilee samalla protonin. ^{14}C hajoaa \beta^{-}-hajoamisella. Kirjoita isotoopin ^{14}C syntymisen ja hajoamisen reaktioyhtälöt. 4 p.
8.2 Arkeologisten orgaanisten näytteiden, kuten nuotiohiilien ja eläinten luiden, ikä voidaan arvioida näytteessä olevien hiilen isotooppien avulla. Selitä lyhyesti, mihin tämä radiohiiliajoitus perustuu. 4 p.
8.3 Eräästä Itä-Suomessa sijaitsevasta kivikautisesta asuinpaikasta löytyi kaivauksissa nisäkkään luu, jolle tehtiin massaspektrometrillä hiilen isotooppisuhteiden määritys. Isotooppien ^{14}C ja ^{13}C lukumääräsuhteeksi saatiin 3{,}5\cdot 10^{-11}. Arvioi, kuinka kauan aikaa sitten asuinpaikkaa käytettiin. 7 p.
Osa 3: 20 pisteen tehtävät
Vastaa kahteen tehtävään.9. Diodi 20 p.
9.1 Kerro, kuinka diodi käyttäytyy virtapiirissä. Mihin diodeja käytetään? 6 p.
9.2 Suunnittele ja kuvaile mittaus, jolla voit määrittää tuntemattoman diodin ominaiskäyrän. Sinulla on käytössäsi diodin lisäksi johtimia, jännitemittari, välillä 0–5 V säädettävä tasajännitelähde sekä useita erilaisia vastuksia, joiden resistanssit tunnetaan. Millaisen ominaiskäyrän oletat saavasi tulokseksi? 14 p.
10. Saippuakuplat 20 p.
10.1 Auringonvalo heijastuu kuplien pinnoista. Selitä, miksi heijastuneessa valossa näkyy eri värejä. 5 p.
10.2 Selitä, miksi kuplan värit vähitellen haalistuvat ja juuri ennen kuplan puhkeamista häviävät miltei kokonaan. 3 p.
10.3 Saippuakupla puhkeaa yleensä muutamassa minutissa. Miksi se puhkeaa? Samasta määrästä nestettä voidaan puhaltaa erikokoisia kuplia. Miksi isot kuplat puhkeavat nopeammin kuin pienet kuplat? 4 p.
10.4 Fyysikko huomaa, että yksi kuplista leijuu paikallaan tyynessä ilmassa. Saippuaveden tiheydeksi oletetaan 1{,}0\cdot 10^3 kg/m3 ja kuplan sisällä olevan ilman lämpötilaksi 26 °C. Ulkoilman lämpötila on 21 °C ja ja kuplan säde 5,0 cm. Määritä näillä tiedoilla kuplan kalvon paksuus. Ilman oletetaan olevan 79 % typpeä ja 21 % happea myös kuplan sisällä. 8 p.
11. Juoman jäähdyttäminen 20 p.
11.1 Ensimmäisessä kokeessa kolme juomaa laitetaan jääkaappiin. Miksi juomat jäähtyvät eri tahtiin? 4 p.
11.2 Toisessa kokeessa juomat kääritään märkään paperiin. Miksi paperikääre tehostaa jäähtymistä parvekkeella enemmän kuin jääkaapissa? 4 p.
11.3 Kolmannessa kokeessa juomat viilennetään jääkylvyssä. Miksi jääkylpy viilentää juomia nopeasti, ja miksi suolan lisääminen vaikuttaa viilenemisnopeuteen? 4 p.
11.4 Viimeisenä esitetään ajatuskoe, jossa litra olutta (T = 25\ ^\circ\mbox{C}) jäähdytetään putkessa. Oleta, että putken säde on 6 cm. Kuinka korkea putken pitäisi olla, jotta juoma voitaisiin jäähdyttää lämpötilaan 9 °C? Voit olettaa, että juoma vastaa ominaisuuksiltaan vettä ja vain pieni osa vedestä höyrystyy. 8 p.
Kokeen tehtävät loppuvat tähän.
Lähteet
- Lähde: YTL.
- Lähde: YTL.
- Lähde: YTL.
- Lähde: Sinituote Oy. https://sinituote.fi/wp-content/uploads/2017/07/1560_polyhuiska.jpg. Viitattu: 23.10.2021. Muokkaus: YTL.
- Lähde: YTL.
- Lähde: YTL.
- Lähde: YTL.
Tarkista, että vastasit ohjeiden mukaiseen määrään tehtäviä. Älä jätä mitään merkintöjä sellaisen tehtävän vastaukselle varattuun tilaan, jota et halua jättää arvosteltavaksi.